
R ile Enerji Analizi ┬ľ B├Âl├╝m 7- ├ťssel D├╝zg├╝nle┼čtirme, Mevsimsellik ve Trend (ETS, STL) ile Elektrik Talep Tahmini Denemesi
├ľzet: Bu b├Âl├╝mde, 6. B├Âl├╝m├╝n devam─▒ ┼čeklinde teorisine fazlaca girmeden, Rob J. Hyndman taraf─▒ndan haz─▒rlanan Forecast paketi ile baz─▒ tahmin modellerini inceleyece─čiz. Bu b├Âl├╝mde ├Âzellikle ├╝ssel d├╝zg├╝nle┼čtirme (exponential smoothing), Loess ile mevsimsel ve trend ayr─▒┼čt─▒rma y├Ântemi (STL, Seasonal and Trend decomposition using Loess) ile otomatik model tahminlerinden sonra ┬ôforecast(┬ô komutu ile modellerimizi ileri ta┼č─▒yarak, kestirim yapmaya ├žal─▒┼čaca─č─▒z.
Bu B├Âl├╝mdeki Fonksiyonlar
read.csv
ts(veri, start=ba┼člad─▒─č─▒ tarih, frequency= periyodu)
decompose(veri seti)
stl(veri seti, parametreler)
ses(veri seti)
forecast(model, h=tahmin miktar─▒)
hw(veri seti)
stlf(veri seti)
7.0. Veriyi y├╝klemek
Her zamanki gibi veri dosyam─▒z─▒ tekrar y├╝kleyelim.
veri=read.csv("http://www.barissanli.com/calismalar/dersler/r/elektrik-talep.csv",
header=TRUE,sep=";",dec=".")
Ortalama t├╝ketim verisini de ot de─či┼čkenine atayal─▒m.
ot=veri$ortalama_tuketim
├×imdi ┬ôveri┬ö yazd─▒─č─▒m─▒z her noktada alt detaylara eri┼čebiliriz. Ders 6┬ĺda
oldu─ču gibi forecast paketini bilgisayar─▒n─▒za kurdu─čunuza emin olun. Daha ├Ânce kurmad─▒ysan─▒z:
install.packages(“forecast”)
─░le kurabilirsiniz.
7.1. Zaman Serileri
E─čer zaman serileri kullanacak isek, ├Ânce yukar─▒da y├╝kledi─čimiz ot de─či┼čkenini bir zaman serisi olarak belirtmekte fayda var. Bu ise gayet basit bir ┼čekilde yap─▒labiliyor. Bunun i├žin ┬ôts┬ö komutunu kullanaca─č─▒z.
library("forecast")
ot=veri$ortalama_tuketim
ott=ts(ot)
![]()
Veri her ne kadar zaman serisi olarak basit├že tan─▒mlan─▒yor olsa da, zaman serisini biraz daha detayl─▒ tan─▒mlayabiliriz. Hat─▒rlanaca─č─▒ ├╝zere ┬ôveri┬ö de─či┼čkenimiz 1 Ocak 2007┬ĺden ba┼člayarak, g├╝nl├╝k olarak devam eden bir veri setiydi. Bu y├╝zden zaman serimizi biraz daha detayl─▒ tan─▒mlayal─▒m. Bunun i├žin, 2007 ba┼č─▒ndan ba┼člad─▒─č─▒ i├žin ┬ôstart=2007┬ö, 365 g├╝nde bir devretti─či i├žin de ┬ôfrequency=365┬ö parametrelerini ekleyelim.
ott=ts(ot,start=2007,frequency=365)
plot(ott)
![]()
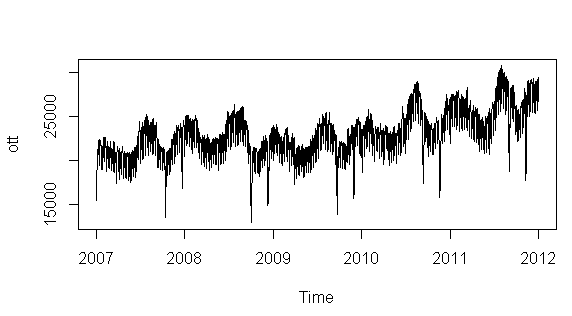
Bir seriyi zaman serisi olarak tan─▒mlad─▒ktan sonra, ├žizdirdi─čimizde otomatik olarak x ekseninin y─▒llara d├Ân├╝┼čt├╝─č├╝n├╝ g├Ârebilirsiniz.
Art─▒k zaman serimiz haz─▒r oldu─čuna g├Âre ├žal─▒┼čmaya ba┼člayabiliriz.
7.2. Seriyi Bile┼čenlerine Ay─▒rmak ┬ľ Decompose
(Konuyla ilgili a├ž─▒klamalar─▒ https://www.otexts.org/fpp/6/1 adresinden bulabilirsiniz.)
Daha ├Ânceki b├Âl├╝mlerde decompose ile bir veriyi bile┼čenlerine ay─▒rm─▒┼čt─▒k.
plot(decompose(ott))
![]()
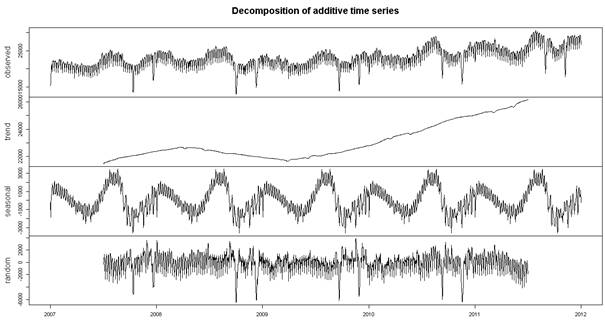
├×imdi ise bir di─čer y├Ântem olan stl┬ĺdir. ┬ôSeasonal and Trend decomposition using Loess┬ö ba┼č harflerinden olu┼čan STL y├Ânteminde Loess ise do─črusal olmayan ili┼čkileri hesaplama y├Ântemidir.
Bir de stl ile deneyelim.
plot(stl(ott,s.window = "periodic"))
![]()
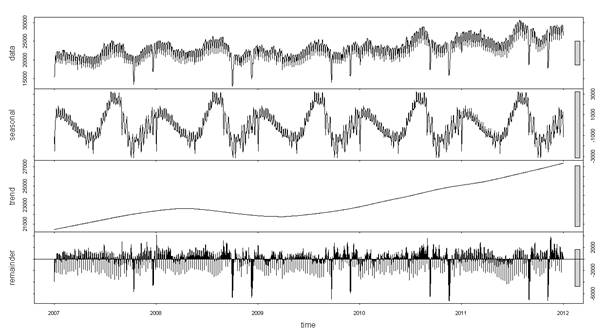
Tabii, daha ba┼čka y├Ântemler de var. Fakat ┼čimdilik bu iki komut i┼čimizi g├Ârecektir. Fakat dikkat edin, T├╝rkiye elektrik talep serisi hem 365 g├╝nl├╝k bir periyoda hem de 354 g├╝nl├╝k ┬ôhicri┬ö bir periyorda daha sahiptir.
7.3. ├ťssel D├╝zg├╝nle┼čtirme ┬ľ Exponential Smoothing
(Konuyla ilgili a├ž─▒klamalar─▒ https://www.otexts.org/fpp/7/1 adresinden bulabilirsiniz.)
Exponential Smoothing┬ĺde basit bir exponential smoothing deneyecek isek,
fit1<-ses(ott)
yeterli olacakt─▒r. Hesaplanan modeli ileri g├Ât├╝rmek/tahmin yapmak i├žin ise ┬ôforecast┬ö fonksiyonunu kullan─▒r─▒z. Burada forecast fonksiyonunda ┬ôh=10┬ö de─čeri ile de 10 ad─▒m ileriye kestirim yapar─▒z..
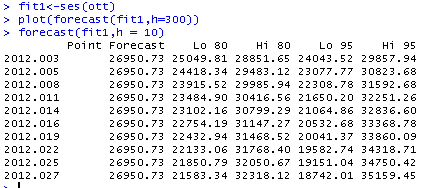
├çizdirmek i├žin ise, ┬ôplot┬ö alan─▒n─▒ s─▒n─▒rland─▒rmam─▒z gerekecek.
![]()
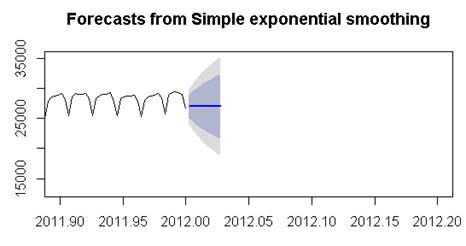
Bu basit exponential smoothing y├Ântemi ├žok ba┼čar─▒l─▒ g├Âz├╝km├╝yor olabilir. ├ç├╝nk├╝ mevsimselli─čin oldu─ču yerlerde ├žok da ba┼čar─▒l─▒ de─čil, fakat daha k─▒sa zaman aral─▒klar─▒ var ise o zaman daha ba┼čar─▒l─▒ olabilir. Bu y├╝zden bir de ┬ôottw┬ö yani haftal─▒k bir de─či┼čken tan─▒mlayal─▒m. (Burada 24┬ĺten b├╝y├╝k periyodlarda sorun olmaktad─▒r)
ottw=ts(ott,frequency=7)
├×imdi kestirim yapmay─▒ deneyelim.
ottw=ts(ott,frequency=7)
fit2<-ses(ottw)
plot(forecast(fit2,h=300),xlim=c(255,265))
![]()
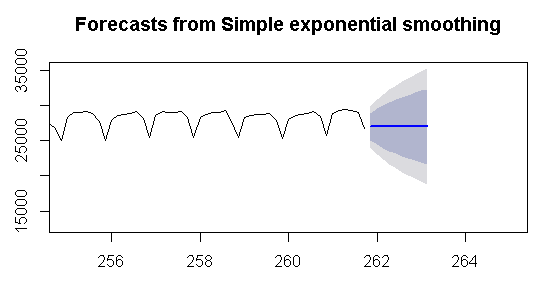
Dikkat ederseniz fonksiyonumuzu y─▒ll─▒ktan haftal─▒─ča ├ževirdi─čimizde x ekseni de de─či┼čmektedir.
├×imdi bir de Holt Winters y├Ântemini deneyelim. Yine haftal─▒k frekansl─▒ verimizi kullan─▒yoruz. Bunun i├žin ┬ôhw┬ö komutunu kullanaca─č─▒z.
fit3<-hw(ottw)
plot(forecast(fit3,h=300),xlim=c(255,265))
![]()
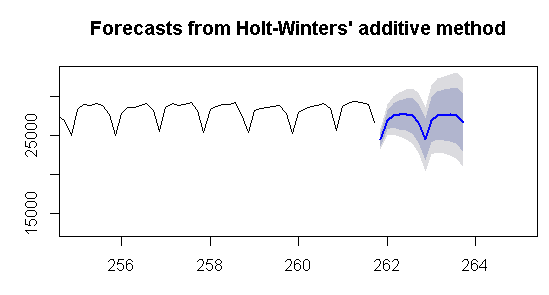
Ba┼čl─▒ktan da anlayabilece─činiz ├╝zere Holt Winters┬ĺin ┬ôadditive┬ö y├Ântemi ile bir grafik olu┼čtu. Fakat Holt Winters┬ĺi ┬ômultiplicative┬ö denemek istersek,┬á
seasonal=”multiplicative”
parametresini ekleriz.
fit3<-hw(ottw,seasonal = "multiplicative")
plot(forecast(fit3,h=300),xlim=c(255,265))
![]()
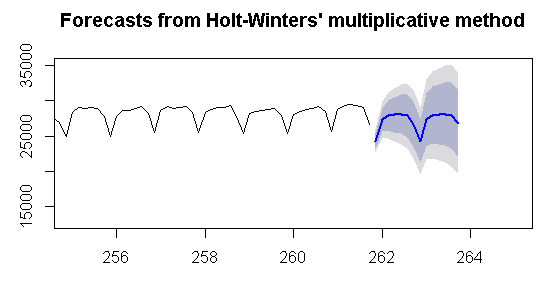
7.4. ├ťssel D├╝zg├╝nle┼čtirme Modelinin Otomatik Belirlenmesi
Modeller, testler derken kendimizi bir s├╝r├╝ karma┼čan─▒n i├žinde bulabiliriz. ┬ôforecast┬ö paketindeki bir komut t├╝m bunlar─▒ otomatik hale getirmekte ve bizim yerimize en ba┼čar─▒l─▒ modeli se├žmektedir.
├ľnce modeli hesaplatal─▒m
fit4<-ets(ottw)
plot(forecast(fit4,h=300))
![]()
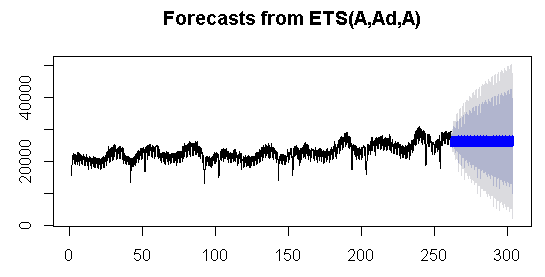
Biraz daha yak─▒ndan bakal─▒m:
plot(forecast(fit4,h=300),xlim=c(258,285))
![]()
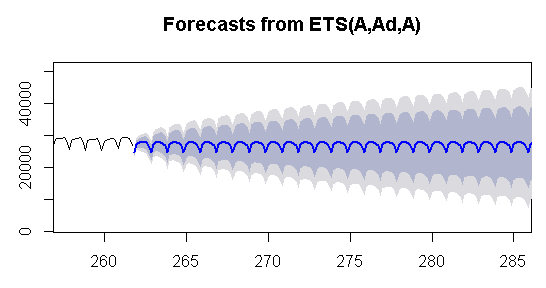
┬ôets┬ö komutunun otomatik olarak se├žti─či parametreler, grafi─čin ba┼čl─▒─č─▒nda g├Âz├╝kmektedir. Uzun sezonsal e─čilimleri olan veriler i├žin uygun g├Âz├╝kmese de, k─▒sa periyotlu verilerde istenene yak─▒n sonu├žlar vermektedir.
7.4. STL ┬ľ Seasonal and Trend decomposition using Loess
Yukar─▒da exponential smoothing┬ĺde g├Âr├╝ld├╝─č├╝ ├╝zere uzun periyotlu mevsimsel trendlere pek de uygun olmad─▒─č─▒ durumlar var. Bunun yerine yine ┬ôforecast┬ö paketindeki stl ve stlf komutlar─▒n─▒ denemekte fayda var.
Veri olarak 365 periyotlu ott verisini kullanaca─č─▒z. Burada ├Ânceki b├Âl├╝mde kulland─▒─č─▒m─▒z stl yerine stl forecast olarak stlf┬ĺi kullanaca─č─▒z. ┬ôstlf┬ö┬ĺe sadece veri setini vererek sonucu g├Âzlemleyece─čiz.
fit5<-stlf(ott)
plot(forecast(fit5,h=300))
![]()
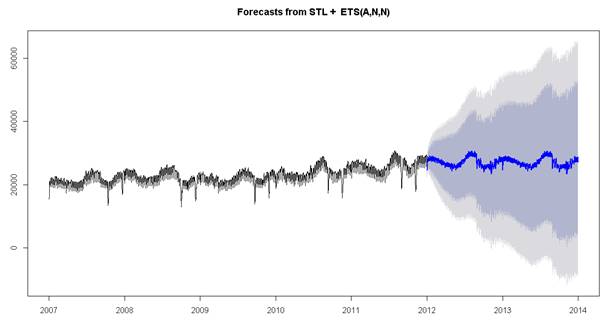
G├Âr├╝ld├╝─č├╝ ├╝zere stlf komutu ile ├žok daha ba┼čar─▒l─▒ bir forecast elde etmi┼če benziyoruz.
Peki bu kestirim sonu├žlar─▒n─▒ nas─▒l g├Ârece─čiz. Bunun i├žin modeli kestirdikten sonra forecast komutu ile ba┼člayan k─▒sm─▒ plot┬ĺa aktarmak yerine bir ba┼čka de─či┼čkene atal─▒m. Sonra bu verinin i├žeri─čine bakal─▒m.
verif=forecast(fit5,h=300)
str(verif)
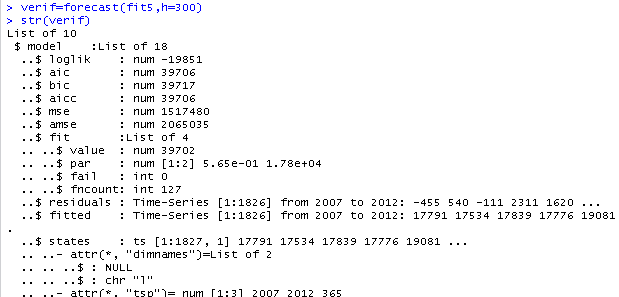
Ekrana t├╝m alt de─či┼čkenler s─▒─čmad─▒─č─▒ndan yer veremedi─čimiz, daha altlarda bir ┬ômean┬ö de─či┼čkeni var.
E─čer bu de─či┼čkeni ├ža─č─▒r─▒rsak da sadece hesaplanan tahmini g├Ârebiliriz.
plot(verif$mean)
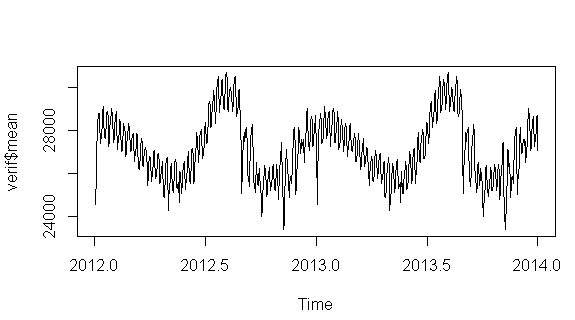
Verilerimizin:
- Kulland─▒─č─▒m─▒z de─či┼čkenleri x┬ĺde yani verif$x┬ĺde
- Hesaplanan kestirim de─čerleri de mean┬ĺde yani verif$mean┬ĺde
─░ki seriyi birle┼čtirirmek i├žin de sadece yeni bir vekt├Âr tan─▒mlayarak iki veriyi arka arkaya virg├╝lle s─▒ral─▒yoruz.
tumveri=c(verif$x,verif$mean)
plot (tumveri,type="l")
![]()
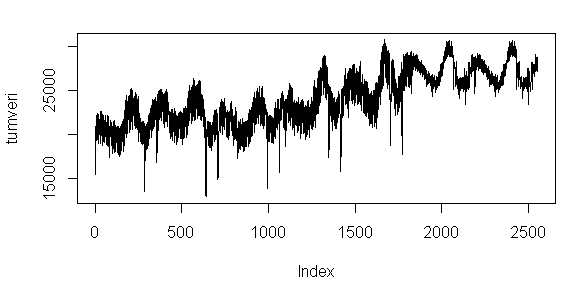
G├Âr├╝ld├╝─č├╝ ├╝zere t├╝m bir seriyi bir araya getirdi─čimizde kestirimi yap─▒lan k─▒sm─▒n, tarihsel veriden daha az varyans─▒ oldu─ču d├╝┼č├╝n├╝lebilir.
├×imdi t├╝mveriyi bir zaman serisi olarak 2007┬ĺden ba┼člayan ve g├╝nl├╝k de─či┼čen bir veri olarak de─čerlendirerek bir kez daha ├žizelim.
plot (ts(tumveri,start=2007,frequency=365),type="l")
![]()
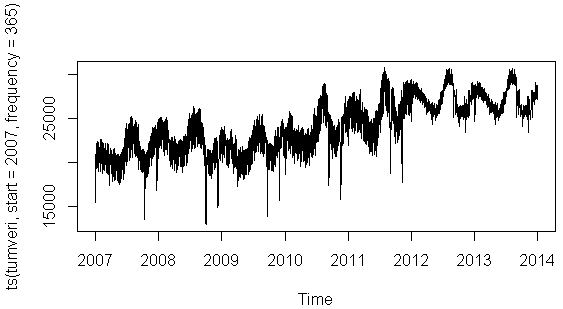
Elde etti─čimiz bu veriyi ┼čimdi bir kez daha bile┼čenlerine ay─▒ral─▒m, bakal─▒m matematiksel hesaplamalar nas─▒l bir trend ve mevsimsellik hesab─▒ yapm─▒┼č.
tumverit=ts(tumveri,start=2007,frequency=365)
plot(decompose(tumverit))
![]()
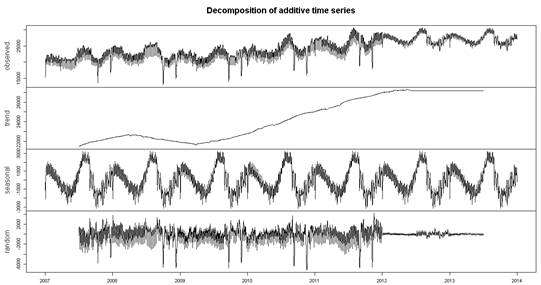
Bekledi─čimiz gibi modelin 2012┬ĺden ├Ânceki ger├žekle┼čmelerindeki mevsimsellik aynen al─▒narak, trend ayn─▒ ┼čekilde devam ettirilmi┼č. Fakat random yani ger├žek verideki hesaplanamayan k─▒s─▒m yerine hemen hemen hi├žbir┼čey eklenememi┼č ve dolay─▒s─▒yla model kestirimi daha ┬ôsade┬ö olmu┼čtur.
Sonu├ž
Bu b├Âl├╝mde ise exponential smoothing ve mevsimse ve trend y├Ântemleri incelenmi┼čtir. Modelimiz g├Âr├╝ld├╝─č├╝ kadar─▒ ile daha stabil g├Âz├╝kmekle birlikte, ┬ôforecast┬ö paketinin bize sa─člad─▒─č─▒ en ├Ânemli kolayl─▒k modelin otomatik se├žilmesini sa─člayan ets() ve stlf() komutlar─▒ olmu┼čtur.
E─čer fonksiyonlar─▒n sonu├žlar─▒n─▒ de─či┼čtirmek isterseniz, ├ž─▒kt─▒lar─▒ bir de─či┼čkene alarak alt de─či┼čkenlerden de─či┼čiklikler yapabilirsiniz. Mesela trend┬ĺini de─či┼čtirme imkan─▒n─▒z var.
Yine i├žeride ge├žen bir ├žok k─▒saltmay─▒ uzun uzuday─▒ anlatmad─▒k. Bunlar─▒n hepsi Hyndman┬ĺ─▒n kitab─▒nda https://www.otexts.org/fpp/7/6 yer almaktad─▒r.
├ľzellikle ┬ô7.6 A taxonomy of exponential smoothing methods┬ö┬ĺda g├Ârd├╝─č├╝m├╝z A,Ad,N ne demek a├ž─▒klamalar─▒ bulabilirsiniz.
Tahmin yaparken en ├Ânemli konulardan biri de ┬ômatematiksel modellere k├Âr├╝ k├Âr├╝ne saplanmamaktad─▒r┬ö. Sonunda en iyi tahminler uzman g├Âr├╝┼č├╝ + iyi matematiksel modellerle olu┼čturulmaktad─▒r.
Komutlar
veri=read.csv("http://www.barissanli.com/calismalar/dersler/r/elektrik-talep.csv", header=TRUE,sep=";",dec=".")
library("forecast")
ot=veri$ortalama_tuketim
ott=ts(ot)
ot_t=ts(ot,start=2007,frequency=365)
plot(ott)
plot(decompose(ott))
plot(stl(ott,s.window = "periodic"))
fit1<-ses(ott)
plot(forecast(fit1,h=300))
fit1<-ses(ott)
plot(forecast(fit1,h=300))
forecast(fit1,h = 10)
plot(forecast(fit1,h=300),xlim=c(2011.9,2012.2))
ottw=ts(ott,frequency=7)
fit2<-ses(ottw)
plot(forecast(fit2,h=300),xlim=c(255,265))
fit3<-hw(ottw)
plot(forecast(fit3,h=300),xlim=c(255,265))
fit3<-hw(ottw,seasonal = "multiplicative")
plot(forecast(fit3,h=300),xlim=c(255,265))
fit4<-ets(ottw)
plot(forecast(fit4,h=300))
fit4<-ets(ottw)
plot(forecast(fit4,h=300),xlim=c(258,285))
fit5<-stlf(ott)
plot(forecast(fit5,h=300))
verif=forecast(fit5,h=300)
str(verif)
plot(verif$mean)
tumveri=c(verif$x,verif$mean)
plot (tumveri,type="l")
plot (ts(tumveri,start=2007,frequency=365),type="l")
tumverit=ts(tumveri,start=2007,frequency=365)
plot(decompose(tumverit))